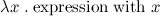Очень люблю Inkscape, и часто в нём рисую разные схемы. А для того, чтобы рисовать схемы, нужны стрелки. Готового инструмента «стрелка» в Инкскейпе нет*, поэтому творю из подручных материалов сообразно вкусу и потребностям. В общем-то, минутное дело, умеючи...
Я подумал, что кому-то, возможно, будет интересно увидеть, как можно самому нарисовать практически любую стрелку. Предлагаю небольшой видеоурок, где показываю как нарисовать стрелку попроще и стрелку позатейливей:
* В инкскейпе есть маркеры конца и начала линии. Красить их нельзя, они всегда чёрные. Впрочем, подсказывают из зала, можно — создав стрелку, надо «оконтурить обводку», получить два контура (древко и острие), вручную их подправить-подравнять, и получится полноценная контурная стрелка. Я пока остаюсь приверженцем своего способа создания контурных стрелок. Впрочем, смотрите на другой способ сами (подал идею и сделал видео freedomfidaj).
20090922
20090918
(Новичковые) ужасы Хаскеля
Я — начинающий программист на Хаскеле, и пока я ещё помню всё, чем он страшен. И это хочу записать. Сразу скажу, когда я приступал к Хаскелю, я ещё не знал практически ничего о функциональном программировании, поэтому одновременно с языком, нужно было осваивать новые идеи и образ мысли. И вообще-то это было здорово. А у страха, как известно, глаза велики. В общем, я думаю, эта заметка может быть полезна и другим начинающим. В ней я укажу на пять непонятных мне вначале, но относительно несложных вещей, поняв которые хотя бы приблизительно, освоить язык мне было гораздо легче.
Вообще-то, именно поэтому я и выучил Хаскель. Мне было просто любопытно, что означают все эти лямбды. Очень помогла в самом начале статья Пола Худака Conception, evolution, and application of functional programming languages (PDF также здесь). Возможно, есть введения и получше, но я начинал с него.
Ламбда-выражение — самая суть «функций» — это выражение вида
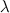 ключевым словом для определения функций. Действительно, когда я и до этого уже пользовался лямбдами в Питоне (и почти во всех других современных языках они тоже есть). В Питоне они выглядят вот так:
ключевым словом для определения функций. Действительно, когда я и до этого уже пользовался лямбдами в Питоне (и почти во всех других современных языках они тоже есть). В Питоне они выглядят вот так:
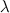 ,
,
Однако тут есть одна тонкость. Как только я начал читать о Хаскеле, я увидел лямбда-выражения, которые поначалу казались немного странными:
В Хаскеле все функции являются функциями одного аргумента. Поначалу это может показаться ограничением, но на деле это очень удобная и практичная идея. Любую функцию n аргументов можно представить как функцию одного аргумента, возвращающую другую функцию n–1 аргементов. И по науке это азывается каррированием. Эта идея, в частности, позволяет передавать функции только часть аргументов.
Узнав об этом, мы теперь можем читать любые выражение с множеством «стрелок»:
Даже эти простые понятия о лямбда-функиях были уже достаточны, чтобы начать пользоваться Хаскелем и понять большинство примеров и объяснений.
По-моему, знак равенства (
В отличии от большинства императивных языков, где
«Равна» — не значит «становится». Это означает, что нечто равно чему-то ещё. Всегда. Как в математике.
Таким образом,
Пользователям функциональных языком это покажется слишком уж очевидным, но именно в смысле знака равенства самое важное изменение для тех, кто раньше пользовался императивными языками. Теперь, кстати, мы можем давать имена нашим безымянным функциям:
Система типов в Хаскеле просто прекрасна. В ней очень легко и естественно выражаются многие идеи. И возможно, именно классы типов — это наименее чуждая концепция для тех, кто приходит в Хаскель из процедурного и объектно-ориентированного мира. Во всяком случае, мне так показалось. Однако классы типов — это совсем не то же самое, что классы в Си++ или в Джаве. Гораздо больше они похожи на абстрактные шаблоны классов в Си++, потому что классы типов
Как только мы привыкнем, что типы классов — это не классы Си++, а абстрактные интерфейсы, и экземпляры классов это не «объекты», а конкретные реализации абстрактных интерфейсов, Хаскель сразу станет привычным и уютным.
Я очень советую почитать вики-статью OOP vs type classes, которая гораздо более детально сравнивает объектно-ориентированный подход и классово-типовой.
Не важно, насколько мягкое введение в Хаскель, рано или поздно его читатель упрётся лбом в крепкую стеную из монад. Да, это вам не плюшки тырить, это вам серьёзная математика. Где-то за этой стеной.
Но вот что я понял: изучать абстрактную математику совсем не обязательно, чтобы монады использовать, а они и правда очень изящная программистская техника. Вначале они казались мне немного странными, но понять раз и навсегда монады гораздо легче, чем запоминать (и правильно применять!) бесчисленные шаблоны ОО-проектирования. Монады логичней.
Поскольку тьюториалов по монадом огромное множество, я не буду их здесь повторять и ожидаю, что вы их уже прочитал парочку. Что же не так с монадами? Для человека, привыкшему к императивным языка, испорченному годами объектно-ориентированного мышления монады кажутся странными. Они выглядят как абстрактный класс-контейнер с загадочным методом
Отвечу вначале на последний вопрос. Зачем нужно связывание (
Самая простая программистская аналогия монадам, которую я придумал, это конвееры (pipes) в командной оболочке Unix. Монады обеспечивают однонаправленный конвеер для вычислений. То же самое делают и конвееры в Unix. Например:
Монады очень похожи.
Как вы уже, наверное, знаете, списки и тип
В большинстве языков
Вторая мнемоника. Функция верхнего уровня любой программы на Хаскеле выполняется в монаде
Надеюсь, что после этих объяснений имя
Следующий вопрос бывшего ОО-программиста, как вытащить значение вычисления из монады?. Начнём с того, что монады преднамеренно спроектированы именно так, что это не всегда возможно. Например, нельзя извлечь чистое значение из монады
Заключение по монадам
Итак, связывание (
Даже спустя месяцы после того, как я начал учить Хаскель, умея написать какие-то полезные программы на нём, я вижу вокруг, в мире Хаскеля, ещё много понятий, о которых не знаю ничего или имею только очень смутное представление. Я называю такие понятия «страшными словами». И я вижу, что есть люди, которые создают и используют библиотеки, воплощающие эти понятия в жизнь.
Надо признать, Хаскель остаётся испытательной площадкой для исследователей. И это одновременно и хорошо, и плохо. Это хорошо, потому что даёт чувство, что передний край науки и технологии очень близок, и можно при желании пользоваться преимуществами новых подходов. При желании. И одновременно это плохо, потому что иногда, когда хочется использовать новую изящную библиотеку, оказывается, что она активно использует незнакомые и не совсем понятные идеи, и нужно быть готовым такие идеи осваивать.
Например, есть современная XML-библиотека HXT. Она очень много использует стрелки. Стрелки — более универсальные комбинаторы вычислений, чем монады, но мне потребовалось гораздо больше, чем один день, чтобы их более-менее понять. Строго говоря, стрелки не являются частью языка, но они — понятие, которое применяют пользователи этого языка. И таких примеров немало. Хотя тем, кому стрелки осваивать не хочется, можно пользоваться более традиционной и активно поддерживаемой XML-библиотекой HaXml.
Я думаю, важно не бояться «страшных слов». К счастью, основополагающие идеи хорошо описаны. Как правило, есть статьи их очень детально объясняющие. Я сам решил осваивать такие идеи по мере необходимости. Это обещает быть и увлекательным, и одновременно посильным.
Я перечислил пять простых идей, освоив которые, мне стало легче привыкнуть к Хаскелю. Лямбды — это просто способ записи функций, и функции нескольких аргументов можно всегда записать как функцию одного, возвращающую другую функцию. Типы классов очень похожи на абстрактные полиморфные интерфейсы в объектно-ориентированном подходе. Монады — стандартизованный способ соединять вычисления вместе. А страшные слова — просто страшные слова. Без них можно жить, но скучно.
Надеюсь, мои заметки будут полезны и ещё кому-нибудь.
Эта статья есть также по-английски. This post is also available in English.
1. Ламбда-функции
— Но мы называем его лембас или путевой хлеб, он подкрепляет лучше, чем любая пища людей, и он гораздо вкуснее.
Вообще-то, именно поэтому я и выучил Хаскель. Мне было просто любопытно, что означают все эти лямбды. Очень помогла в самом начале статья Пола Худака Conception, evolution, and application of functional programming languages (PDF также здесь). Возможно, есть введения и получше, но я начинал с него.
Ламбда-выражение — самая суть «функций» — это выражение вида
Значением этого выражения является пока ещё безымянная функция одного аргумента (x), что-то с ним вычисляющая (а именно, выражение справа от точки). С лямбда-функциями связана серьёзная математическая теория, но с точки зрения программирования можно считать
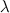 ключевым словом для определения функций. Действительно, когда я и до этого уже пользовался лямбдами в Питоне (и почти во всех других современных языках они тоже есть). В Питоне они выглядят вот так:
ключевым словом для определения функций. Действительно, когда я и до этого уже пользовался лямбдами в Питоне (и почти во всех других современных языках они тоже есть). В Питоне они выглядят вот так:lambda x: expression with xИми было очень удобно пользоваться в
filter() и reduce(). И вообще, почти везде, где в качестве аргумента требуется имя функции. Однако у лямбда-функций нет имён, и именно поэтому их ещё называют анонимными (безымянными) функциями. В пайтоне иногда я давал им имена прямо на лету:add_42 = lambda x: x + 42Теперь имя
add_42 указывает на функцию. Точно такой же результат можно было получить, записав определение функции как обычно:def add_42(x):А что же насчёт Хаскеля? Да почти то же самое. Символ
return x+42
\ заменяет 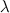 ,
, -> служит вместо точки. Всё вместе записывается так:\x -> выражение с xИ мы даже можем давать имена таким безымянным функциям, так же как и в Питоне:
add_42 = \x -> x + 42Согласитесь, очень похоже.
Однако тут есть одна тонкость. Как только я начал читать о Хаскеле, я увидел лямбда-выражения, которые поначалу казались немного странными:
\x -> \y -> выражение с x и yЧто означают все эти «стрелочки»? Ответ оказался очень прост и очень полезен в дальнейшем освоении языка.
В Хаскеле все функции являются функциями одного аргумента. Поначалу это может показаться ограничением, но на деле это очень удобная и практичная идея. Любую функцию n аргументов можно представить как функцию одного аргумента, возвращающую другую функцию n–1 аргементов. И по науке это азывается каррированием. Эта идея, в частности, позволяет передавать функции только часть аргументов.
Узнав об этом, мы теперь можем читать любые выражение с множеством «стрелок»:
\x -> (\y -> выражение с x и y)Значением такого выражения будет фукнция, берущая один аргумент и производящая другую функцию, которая берёт ещё один аргумент. Такое выражение в целом ведёт себя как функция двух аргументов. Например, мы можем вычислить такую функцию двух аргументов в интерпретаторе Хаскеля
ghci:ghci> (\x -> \y -> x + y ) 3 4Конечно, есть более краткий способ записи функций двух аргументов (обратите внимание, что список аргументов брать в скобки совсем не нужно):
7
ghci> (\x y -> x + y) 3 4Однако знать, что на самом деле все функции нескольких аргументов являются функциями одного аргумента очень полезно. Например, это помогает читать описания типов функций. Например, тип функции
7
map выглядит так:map :: (a -> b) -> [a] -> [b]Я обычно читаю это следующим образом: «функция
map принимает два аргумента, первый — функцию преобразующую a в b, второй — список элементов типа a, а возвращает список элементов типа b». Но иногда гораздо естественнее записать тот же самый тип так:map :: (a -> b) -> ([a] -> [b])«Функция, которая берёт функцию, преобразующую
a в b, и возвращает функцию, преобразующую список a в список b».Даже эти простые понятия о лямбда-функиях были уже достаточны, чтобы начать пользоваться Хаскелем и понять большинство примеров и объяснений.
2. Знак равенства
— Ну что, если тут нет смысла, — сказал Король, — тогда у нас гора с плеч: нам незачем пытаться его найти! Сэкономим кучу работы! И все же...
По-моему, знак равенства (
=) — самый важный символ в Хаскеле. Понять его важно для понимания языка. И мне кажется, смысл равенства недостаточно подчёркивается во всевозможных учебниках. Например, это единственное ключевое слово, отсутствующее в списке ключевых слов Хаскеля в его вики.В отличии от большинства императивных языков, где
= означает присваивание (то есть действие), в Хаскеле он означает, что левая часть равна правой (то есть описывает свойство).Дополнение: в комментариях уточняют, «равно» в Хаскеле — связывание имени слева с определением справа.
«Равна» — не значит «становится». Это означает, что нечто равно чему-то ещё. Всегда. Как в математике.
a = b в Хаскеле означает, что a равно b по определению, a эквивалентно b.Таким образом,
= в Хаскеле служит для записи определений. «Равно» может определять самые разные вещи, но определяет их статично. Оно не зависит от порядка выполнения операций. На него можно положиться.Пользователям функциональных языком это покажется слишком уж очевидным, но именно в смысле знака равенства самое важное изменение для тех, кто раньше пользовался императивными языками. Теперь, кстати, мы можем давать имена нашим безымянным функциям:
add = \x -> \y -> x + yПризнаю, что читается это плохо, поэтому в большинстве случаев функции в Хаскеле определяются так:
add x y = x + yНо и это по-прежнему определение функции
add.3. Классы типов
Significant benefits arise from sharing a common type system, a common toolset, and so forth. These technical advantages translate into important practical benefits such as enabling groups with moderately differing needs to share a language rather than having to apply a number of specialized languages. — приписывается Б. Страуструпу
Система типов в Хаскеле просто прекрасна. В ней очень легко и естественно выражаются многие идеи. И возможно, именно классы типов — это наименее чуждая концепция для тех, кто приходит в Хаскель из процедурного и объектно-ориентированного мира. Во всяком случае, мне так показалось. Однако классы типов — это совсем не то же самое, что классы в Си++ или в Джаве. Гораздо больше они похожи на абстрактные шаблоны классов в Си++, потому что классы типов
- определяют только абстрактный интерфейс
- позволяют создавать несколько независимых реализаций интерфейса (таким образом, для любого типа можно определить экземпляр класса, если предоставить реализацию его методов)
- полиморфны по своей природе и поддерживают наследование
- не могут иметь переменных состояния
Как только мы привыкнем, что типы классов — это не классы Си++, а абстрактные интерфейсы, и экземпляры классов это не «объекты», а конкретные реализации абстрактных интерфейсов, Хаскель сразу станет привычным и уютным.
Я очень советую почитать вики-статью OOP vs type classes, которая гораздо более детально сравнивает объектно-ориентированный подход и классово-типовой.
4. Монады
И так как всякое настоящее состояние простой субстанции, естественно, есть следствие ее предыдущего состояния, то настоящее ее чревато будущим, — Лейбниц, «Монадология»
Не важно, насколько мягкое введение в Хаскель, рано или поздно его читатель упрётся лбом в крепкую стеную из монад. Да, это вам не плюшки тырить, это вам серьёзная математика. Где-то за этой стеной.
Но вот что я понял: изучать абстрактную математику совсем не обязательно, чтобы монады использовать, а они и правда очень изящная программистская техника. Вначале они казались мне немного странными, но понять раз и навсегда монады гораздо легче, чем запоминать (и правильно применять!) бесчисленные шаблоны ОО-проектирования. Монады логичней.
Поскольку тьюториалов по монадом огромное множество, я не буду их здесь повторять и ожидаю, что вы их уже прочитал парочку. Что же не так с монадами? Для человека, привыкшему к императивным языка, испорченному годами объектно-ориентированного мышления монады кажутся странными. Они выглядят как абстрактный класс-контейнер с загадочным методом
>>=:class Monad m whereХорошо, если
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
fail :: String -> m a
return — конструктор, то почему такое чудное имя? Если это класс-контейнер, то как из него что-либо извлечь? И какой смысл применять функцию внутри контейнера (а именно это делает метод >>=, называемый также операцией связывания), если мы не можем вытащить результат из этого контейнера?Отвечу вначале на последний вопрос. Зачем нужно связывание (
>>=)? Монады являются и одновременно не являются контейнерами. Они — обёртки, упаковки для вычислений, а не для значений (return). Однако они обёртывают вычисления не для того, чтобы их было удобнее хранить в монадных коробочках, а чтобы их можно было удобнее соединять друг с другом. Вместо «коробочек» представьте обыкновенные кирпичи, которые ровно кладутся друг к другу. Это, кстати, похоже на шаблон Adapter в ОО-проектировании. Каждая монада определяет какой-то способ передавать результат от одного вычисления к другому и реализует стандартный интерфейс, чтобы этот способ использовать (>>=). И что бы ни случилось, результат всегда останется в той же монаде (даже, если произойдёт сбой, fail).Самая простая программистская аналогия монадам, которую я придумал, это конвееры (pipes) в командной оболочке Unix. Монады обеспечивают однонаправленный конвеер для вычислений. То же самое делают и конвееры в Unix. Например:
$ seq 1 5 | awk '{print $1 " " $1*$1*$1 ;}'
1 12 83 274 645 125seq создаёт список целых чисел. awk вычислят куб каждого из них. Что здесь замечательного? У нас есть две слабо связанные друг с другом программы, которым мы можем легко указать работать вместе. Поток текста создаваемый программой слева попадает по конвееру в программу справа, которая может читать этот поток, что-то с ним делать и создавать уже новый текстовый поток. Текстовый поток — общий формат для результата вычислений, | — операция, связывающая их воедино.Монады очень похожи.
>>= берёт внутреннее вычисление из монады слева и подставляет его в вычисление справа, которое всегда должно создавать ещё одну монаду того же типа.Как вы уже, наверное, знаете, списки и тип
Maybe в Хаскеле — монады. Например, пусть у нас есть простое вычисление, которое возвращает пару из числа и его куба обратно в монаду (return):\x -> return (x, x^3)тогда мы можем взять список и направить его «по конвееру» в это вычисление:
ghci> [1,2,3,4,5] >>= \x -> return (x,x^3)Заметьте, что мы получили список пар. Это та же самая исходная монада (то есть список). Однако если мы возмьём значение
[(1,1),(2,8),(3,27),(4,64),(5,125)]
Maybe и направим его в то же вычисление, на выходе у нас будет та же сама монада Maybe:ghci> Just 5 >>= \x -> return (x,x^3)Таким образом, мы можем создать конвеер из двух вычислений, и поведение этого конвеера зависит от контекста (т.е. от того, какая монада используется), а не от самих вычислений. В отличии от юниксовых конвееров, монады строго типизованы, и сама система типов заботится о том, чтобы выход одной монады был совместим с входом другой. И в отличии от юниксовых конвееров, мы можем задавать наши собственные правила связывания (
Just (5,125)
>>=). Например, такие: «не делать более 42 вычислений подряд» или «посмотреть на входное значение, сделать то или это». Классы монад содержат в себе подобные правила, как соединять вычисления.Дополнение: в комментариях подсказывают, что гораздо более подробно и более строго аналогия между юниксовым конвеером и монадами разобрана в статье Monadic i/o and UNIX shell programming.Теперь, я надеюсь, вы понимаете монады не хуже меня (не обязательно полностью). Хочу обсудить несколько мнемонических правил. Почему
return называется return?В большинстве языков
return возвращает результат вычисления из функции. В Хаскеле же он конструктор для монад. Это очень странно. Однако посмотрим как работает >>=: эта операция извлекает значение из монады слева, а затем связывает его с аргументом функции справа (отсюда, кстати, и другое название метода — bind). А функция справа должна вернуть значение обратно в монаду, чтобы можно было передать эстафетную палочку дальше следующей операции >>=. Это первое мнемоническое правило: return — возвращает вычисленное значения обратно в монаду.Вторая мнемоника. Функция верхнего уровня любой программы на Хаскеле выполняется в монаде
IO (тип функции main — IO ()). Эта монада позволяет выполнять ввод-вывод и вообще любые последовательные действия. Таким образом, монадный код выполняется на самом верхнем уровне программы, и именно он вызывает любой «чистый» код по мере необходимости, а не наоборот. Таким образом, любое «чистое» значение, если не отбрасывается, то рано или поздно возвращается в монаду её вызвавшую.Надеюсь, что после этих объяснений имя
return для монадного конструктора больше не кажется таким уж странным. Я, однако, не утверждаю, что мои объяснения 100% технически верны.Следующий вопрос бывшего ОО-программиста, как вытащить значение вычисления из монады?. Начнём с того, что монады преднамеренно спроектированы именно так, что это не всегда возможно. Например, нельзя извлечь чистое значение из монады
IO. Если дана такая «односторонняя» монада, то всё, что можно с ней делать — передавать внутреннее значение по монадному конвееру дальше. В Хаскеле разработан специальный синтаксис с ключевым словом do, которые делает такую многократную передачу монады по конвееру очень похожей на последовательную императивную программу. Следующие две программы делают одно и то же. Первая записана с do-нотацией:main :: IO ()а вторая явно использует
main = do
name <- getLine
putStrLn ("Hi, " ++ name)
>>=:main :: IO ()Эквивалентная программа на Питоне:
main = getLine >>= \name -> putStrLn ("Hi, " ++ name)
from sys import stdin, stdoutОднако иногда вытащить чистое значение из монадного вычисления можно. Это не предусмотрено общим монадным интерфейсом, поэтому разработчик монады должен специально предусмотреть возможность извлекать значения наружу. Например, можно извлекать значения из монады
if __name__ == "__main__":
name = stdin.readline()
stdout.write("Hi, " + name)
Maybe, используя функцию fromMaybe:ghci> fromMaybe 0 $ Just 3
3
ghci> fromMaybe 0 $ Nothing
0
Заключение по монадам
Итак, связывание (
>>=) позволяет объединять различные монадные вычисления вместе. Почти везде, где есть цепь вычислений, монады очень подходят. Конкретные реализации монад могут содержать разные правила комбинирования вычислений. Имя метода return сбивает с толку начинающих, это метод возвращает результа вычисления обратно в монаду, а не из монады. В общем, когда я понял эти простые идеи, это сильно помогло.5. Страшные слова
Я знаю только то, что ничего не знаю.
Даже спустя месяцы после того, как я начал учить Хаскель, умея написать какие-то полезные программы на нём, я вижу вокруг, в мире Хаскеля, ещё много понятий, о которых не знаю ничего или имею только очень смутное представление. Я называю такие понятия «страшными словами». И я вижу, что есть люди, которые создают и используют библиотеки, воплощающие эти понятия в жизнь.
Надо признать, Хаскель остаётся испытательной площадкой для исследователей. И это одновременно и хорошо, и плохо. Это хорошо, потому что даёт чувство, что передний край науки и технологии очень близок, и можно при желании пользоваться преимуществами новых подходов. При желании. И одновременно это плохо, потому что иногда, когда хочется использовать новую изящную библиотеку, оказывается, что она активно использует незнакомые и не совсем понятные идеи, и нужно быть готовым такие идеи осваивать.
Например, есть современная XML-библиотека HXT. Она очень много использует стрелки. Стрелки — более универсальные комбинаторы вычислений, чем монады, но мне потребовалось гораздо больше, чем один день, чтобы их более-менее понять. Строго говоря, стрелки не являются частью языка, но они — понятие, которое применяют пользователи этого языка. И таких примеров немало. Хотя тем, кому стрелки осваивать не хочется, можно пользоваться более традиционной и активно поддерживаемой XML-библиотекой HaXml.
Я думаю, важно не бояться «страшных слов». К счастью, основополагающие идеи хорошо описаны. Как правило, есть статьи их очень детально объясняющие. Я сам решил осваивать такие идеи по мере необходимости. Это обещает быть и увлекательным, и одновременно посильным.
Заключение
Я перечислил пять простых идей, освоив которые, мне стало легче привыкнуть к Хаскелю. Лямбды — это просто способ записи функций, и функции нескольких аргументов можно всегда записать как функцию одного, возвращающую другую функцию. Типы классов очень похожи на абстрактные полиморфные интерфейсы в объектно-ориентированном подходе. Монады — стандартизованный способ соединять вычисления вместе. А страшные слова — просто страшные слова. Без них можно жить, но скучно.
Надеюсь, мои заметки будут полезны и ещё кому-нибудь.
Эта статья есть также по-английски. This post is also available in English.
20090908
Ещё одна библиотека комбинаторного парсинга
Не так давно я писал о библиотеке
В общем-то, я посмотрел на новую библитечку, и она мне тоже понравилась. Подкупает сравнительная простота самой библиотеки, ясные исходники и подробно написанные руководства — понять как работает библиотека нетрудно. Правда, при чтении документации нужно быть знакомым с нотацией типов, принятой в Haskell (
Комбинаторов в библиотеке всего-то:
Для пробы я решил написать пример разбора того же файлового формата, что и в заметке о pyparsing. Мне кажется, что наиболее эффективно применять
Полный текст примера с тестами кладу в pastebin. Далее пояснения.
Половина кода пришлась на разбор чисел. Вообще, по-моему, в такого рода библиотеках было бы хорошо класть готовые парсеры для чисел, дат, e-mail и тому подобных обыденных вещей где-нибудь в разделе contrib... Впрочем, написать разбор чисел было даже занятно.
Чтение знака числа. Если ни плюса, ни минуса нет, подразумеваю плюс. Волшебный комбинатор
Целые числа состоят из знака и последовательности цифр. Так и запишем:
Здесь я пользуюсь опять комбинатором
Аналогично строю и парсер для рациональных чисел, только прибавляю ещё и дробь, и, соответственно, ещё две вспомогательных функции:
Вот и всё. Использовать примерно так:
Второй половиной кода оказалось написание парсеров для аналогов
После этих определений собственно парсер выбранного формата укладывается в три выражения:
Смотрим на результат:
В общем, впечатления хорошие. Документация у библиотеки приличная. Использовать приятно. Только одно досадное неудобство было связано с тем, что
Тонкости: нужно быть осторожным, не помещая универсально успешный парсер внутрь
См. также заметку про pyparsing.
Дополнение: слайды презентации funcparserlib на DevConf 2010:
pyparsing для комбинаторного парсинга в Python. В комментариях появилась ссылка на ещё одну библиотеку, о которой я вначале не знал, а именно на funcparserlib, написанную Андреем Власовских.В общем-то, я посмотрел на новую библитечку, и она мне тоже понравилась. Подкупает сравнительная простота самой библиотеки, ясные исходники и подробно написанные руководства — понять как работает библиотека нетрудно. Правда, при чтении документации нужно быть знакомым с нотацией типов, принятой в Haskell (
ArgType -> ResultType). Общее впечатление: имеющиеся в funcparserlib комбинаторы практически полностью ортогональны друг другу, записываются кратко, места на экране занимают мало, называются понятно.Комбинаторов в библиотеке всего-то:
some, a, many, finished, maybe, skip, oneplus, forward_decl, +, | и >>. Действие большинства комбинаторов угадывается из названия. Рабочие лошадки: some(функция-предикат) берёт токен, удовлетворяющий условию, a(токен) берёт токен, указанный в аргументе, many(парсер), maybe(парсер), oneplus(парсер) — множественное, возможное или хотя бы однократное срабатывание парсера, skip(парсер) отбрасывает всё найденное парсером. Плюс (+) последовательно применяет два парсера, «или» (|) пробует альтернативные варианты, >> подставляет результат парсера в функцию и создаёт новый парсер (очень полезный комбинатор!). Ещё есть tuple для группировки.Для пробы я решил написать пример разбора того же файлового формата, что и в заметке о pyparsing. Мне кажется, что наиболее эффективно применять
funcparserlib с предварительным лексическим анализом (разбиением текста на токены-лексемы). В принципе, готовый токенизатор — часть стандартной библиотеки Python, поэтому это не проблема. Удобная обёртка приведена в руководстве к funcparserlib. Однако мне хотелось написать пример в том же стиле, что и для pyparsing, поэтому в примере ниже я разбираю текст на уровне отдельных символов.Полный текст примера с тестами кладу в pastebin. Далее пояснения.
Половина кода пришлась на разбор чисел. Вообще, по-моему, в такого рода библиотеках было бы хорошо класть готовые парсеры для чисел, дат, e-mail и тому подобных обыденных вещей где-нибудь в разделе contrib... Впрочем, написать разбор чисел было даже занятно.
Чтение знака числа. Если ни плюса, ни минуса нет, подразумеваю плюс. Волшебный комбинатор
>> позволяет обработать результат и сразу подготовить ответ, или -1, или +1:sign = maybe(a("-")|a("+")) >> (lambda c: c == "-" and -1 or +1)Целые числа состоят из знака и последовательности цифр. Так и запишем:
digits = many(some(lambda c: c.isdigit()))int_num = sign + (digits >> to_int) >> mk_int
Здесь я пользуюсь опять комбинатором
>> и двумя вспомогательными функциями. Одна превращает последовательность символов-цифр в число (to_int), другая умножает результат на -1, если необходимо (mk_int). Эти функции вспомогательные, можно пропустить: powers = lambda digs: zip(digs,xrange(len(digs)-1,-1,-1))add_digit = lambda acc, dp: acc+int(dp[0])*10**dp[1]to_int = lambda digs: reduce(add_digit, powers(digs), 0)mk_int = lambda (s,i): s*i
Аналогично строю и парсер для рациональных чисел, только прибавляю ещё и дробь, и, соответственно, ещё две вспомогательных функции:
to_frac = lambda digs: to_int(digs)*1.0/10**len(digs)mk_frac = lambda (s,i,f): s*(i+f)frac_num = sign + (digits >> to_int) + (skip(maybe(a("."))) + (digits >> to_frac)) >> mk_fracВот и всё. Использовать примерно так:
>>> frac_num.parse("-1.25")-1.25Второй половиной кода оказалось написание парсеров для аналогов
Literal и Word из pyparsing. Это необходимо, потому что без токенизации приходится распознавать цепочки токенов. Дополнительно создал парсер ws для пропуска пробелов: pack = lambda cs: ''.join(cs)literal = lambda s: reduce(lambda a,b: a+b, map(a,s)) >> packword = lambda p: oneplus(some(p)) >> packws = skip(many(some(lambda c: c.isspace())))
После этих определений собственно парсер выбранного формата укладывается в три выражения:
varname = word(lambda c: c.isalpha())var = (ws + varname + ws + frac_num + ws)custom_format = skip(literal("Inspection")) + \ws + skip(literal("#")) + \ws + int_num + \ws + skip(literal("SHOULD")) + \ws + skip(literal("Ref. Sys")) + \ws + int_num + \many(var)Смотрим на результат:
$ python test.py < input.txt (2, 1, [('X', 28.749300000000002), ('Y', 78.995999999999995), ('Z', -1.0014000000000001)])В общем, впечатления хорошие. Документация у библиотеки приличная. Использовать приятно. Только одно досадное неудобство было связано с тем, что
setup.py install --prefix=... из дистрибутивного тарбола не сработал как надо. Впрочем, библиотека такая маленькая, что можно положить все три её файла прямо в свой проект, без общесистемной установки.Тонкости: нужно быть осторожным, не помещая универсально успешный парсер внутрь
many, чтобы избежать вечного цикла. Короче, нельзя внутрь many помещать many, maybe и pure. Подробнее — см. FAQ.См. также заметку про pyparsing.
Дополнение: слайды презентации funcparserlib на DevConf 2010:
20090904
Как сделать видеофайл из GIF-а и добавить поля к видео
Для того, чтобы из анимированного GIFа сделать видеофайл, я недавно использовал
Если нужно добавить чёрных полей (до нужного размера), действую примерно так (в данном случае, хочу получить 320×240):
Дополнение: с новыми версиями ffmpeg (например, 0.6.90), поля к видео добавляются с помощью видеофильтра pad:
Я не использую для разделения на кадры ImageMagick (convert), потому что мне кажется, что
(in English)
gifsicle (чтобы разоптимизировать GIF и разбить на кадры) и ffmpeg (чтобы сделать из кадров видео):gifsicle -U --explode "input.gif"
for f in *.gif.* ; do mv "$f" "$f.gif" ; done
ffmpeg -r 25 -i "input.gif.%03d.gif" -sameq -s 320x240 output.flv
Если нужно добавить чёрных полей (до нужного размера), действую примерно так (в данном случае, хочу получить 320×240):
ffmpeg -i input.file -s 320x180 -padtop 30 -padbottom 30 output.file
Дополнение: с новыми версиями ffmpeg (например, 0.6.90), поля к видео добавляются с помощью видеофильтра pad:
ffmpeg -i input.file -vf "scale=320:180,pad=320:240:0:30" output.file
Я не использую для разделения на кадры ImageMagick (convert), потому что мне кажется, что
gifsicle работает быстрее и требует меньше памяти.(in English)
20090903
Как пометить пакеты в Aptitude, чтобы потом удалить
Очень полезная возможность в
Например, нужно поставить какой-то набор пакетов, чтобы собрать программу X из исходников, а потом нужно эти пакеты удалить. При установке помечаем выбранные пакеты какой-то своей меткой (
А потом, когда эти пакеты больше не требуются, их удаляем, выбрав по той же метке:
Поисковый шаблон
Как видно из примера, особенно эта возможность полезна для самостоятельной сборки пакетов и программ из исходников.
P.S. Не помню, есть ли
This post in English
aptitude — пользовательские метки для выбранных пакетов.Например, нужно поставить какой-то набор пакетов, чтобы собрать программу X из исходников, а потом нужно эти пакеты удалить. При установке помечаем выбранные пакеты какой-то своей меткой (
builddeps в моём примере):$ sudo aptitude install --add-user-tag builddeps libчто-то-dev libчто-то-ещё-dev ...
А потом, когда эти пакеты больше не требуются, их удаляем, выбрав по той же метке:
$ sudo aptitude purge '?user-tag(builddeps)'
Поисковый шаблон
?user-tag(метка) можно использовать совместно со всеми другими поисковыми шаблонами. Присваивать метки можно не только при установке (install), но и во многих других операциях.Как видно из примера, особенно эта возможность полезна для самостоятельной сборки пакетов и программ из исходников.
P.S. Не помню, есть ли
--add-user-tag в Ubuntu, но в Debian Lenny (aptitude-0.4.11) точно есть.This post in English
Подписаться на:
Комментарии (Atom)